Основи інженерії штучного інтелекту 10-11 класи

Лінійна регресія - метод машинного навчання

Лінійна регресія — це простий і поширений метод машинного навчання, який використовується для прогнозування залежності між змінними. Модель лінійної регресії шукає пряму, що найкраще описує зв'язок між незалежною змінною (вхідними даними) і залежною змінною (результатом або прогнозом).

Формула лінійної регресії
Лінійна регресія моделює залежність між двома змінними за допомогою рівняння прямої:
y = kx + b
де:

• y — прогнозоване значення,
• x — незалежна змінна (вхід),
• k — кут нахилу (коефіцієнт або вага),
• b — точка перетину з віссю y (зміщення або інтерсепт).

Мета лінійної регресії — знайти такі значення k і b, щоб лінія найкраще відповідала даним, мінімізуючи помилку між реальними і прогнозованими значеннями.

Приклад
Якщо у вас є дані про продажі автомобілів за роками, лінійна регресія може допомогти спрогнозувати продажі на наступний рік на основі цих даних.

Лінійна регресія є одним із найпростіших алгоритмів для прогнозування, і її часто використовують як базову модель.

Припустимо, ви хочете прогнозувати оцінки студентів на основі кількості годин навчання. Для цього можна використати лінійну регресію для моделювання залежності.

Приклад коду:

import numpy as np
from sklearn.linear_model import LinearRegression

# Дані: роки та кількість студентів
years = np.array([[2017], [2018], [2019], [2020], [2021]])
students = np.array([400, 420, 450, 470, 490])

Намалюємо графік за допомогою бібліотеки matplotlib:

import matplotlib.pyplot as plt
plt.plot(years, students, marker='o', linestyle='-', color='b')

Параметри функції plot() означають, що ми будуємо графік по точках із масивом years по вісі X, students по вісі Y. Точки мають бути позначені кружечками (o), лінія має бути суцільною (-), а колір має бути синім (b - blue).

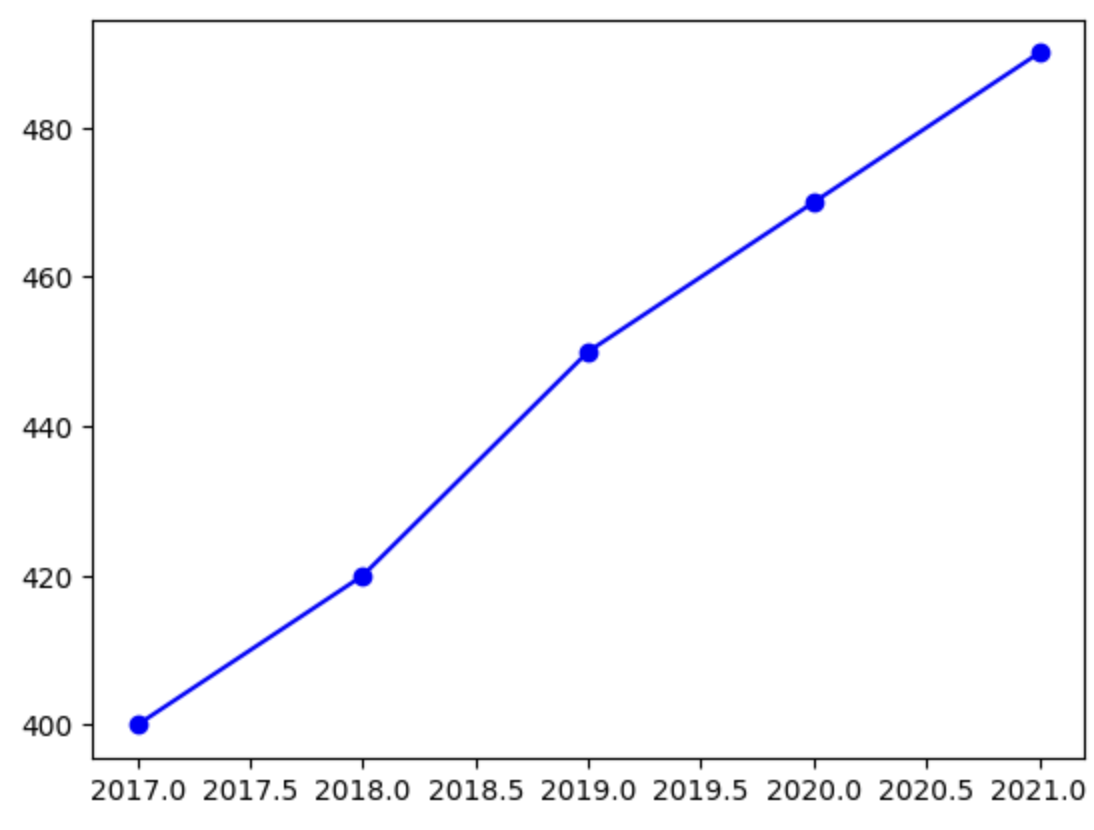
Тепер ми можемо створити модель лінійної регресії, яка підбере параметри прямої так, щоб вона максимально точно відповідала нашим даним:

# Створення та навчання моделі
model = LinearRegression()
model.fit(years, students)

# Прогноз на 2022 та 2023 роки
predictions = model.predict(np.array([[2022], [2023]]))
print(predictions)

Результатом роботи нашої програми буде масив з двох чисел:

array([515., 538.])

що відповідають прогнозній кількості студентів на 2022 та 2023 рік.

Але спочатку, давайте потренуємось працювати із списками.

Завдання №1: Операції зі списками

Дано два списки:

• Список імен студентів: ['Олександр', 'Іван', 'Марія', 'Анна', 'Софія']
• Відповідні оцінки за тест: [78, 85, 88, 90, 92]

Операції:

1. Виведіть ім’я студента, що знаходиться на другій позиції.
2. Виведіть оцінку, яку отримала Анна.
3. Додайте нове ім’я "Віктор" і оцінку 95 до списків.
4. Виведіть оновлений список студентів та їхні оцінки.

Очікуваний результат:

Іван

90

['Олександр', 'Іван', 'Марія', 'Анна', 'Софія', 'Віктор']

[78, 85, 88, 90, 92, 95]

Завдання №2: Операції з масивами NumPy

Створіть масив з оцінками студентів:

import numpy as np
scores = np.array([85, 90, 78, 92, 88, 95, 67, 84, 91, 75])

Операції:

1. Обчисліть середнє значення оцінок:
   mean_score = np.mean(scores)
2. Знайдіть мінімальну та максимальну оцінки:
   min_score = np.min(scores)
max_score = np.max(scores)

Завдання №3: Прогнозуємо розмір мишей за допомогою лінійної регресії

Використовуйте scikit-learn для створення прогнозної моделі розміру мишей на основі їхнього віку.

Дані:

Вимірювання мишей

Вік миші (дні)	Розмір миші (см)	Вага миші (г)
5	3.1	3
10	4.2	6
15	5.0	12
20	5.8	16
25	6.4	22
30	7.0	28
42	7.5	30

Використовуючи ці дані, створіть модель лінійної регресії для прогнозування розміру миші на основі її віку.

Код:

import numpy as np
from sklearn.linear_model import LinearRegression

# Дані
age = np.array([[5], [10], [15], [20], [25], [30]])
size = np.array([3.1, 4.2, 5.0, 5.8, 6.4, 7.0])

# Створення моделі
model = LinearRegression()
model.fit(age, size)

# Прогноз для 35 днів
prediction = model.predict(np.array([[35]]))
print(f"Прогнозований розмір миші для 35 днів: {prediction[0]:.2f} см")

Додаткове завдання:

Використовуючи ці дані, створіть модель лінійної регресії для прогнозування розміру миші на основі її ваги, а не віку. Спрогнозуйте, яка має бути довжина миші, у якої вага - 1 кг?